Finding the scalar potential

The potential in the image problem is obtained by multiplying the Green's function by the charges, and adding them, as usual. However each conductor has an image conductor with equal and opposite charge. Thus the sum of the contributions from an actual line and its corresponding image line is equal to the charge on the actual line times the Green's function for the actual line minus the Green's function for the image line. Thus it is only necessary to sum over actual lines with this difference of Green's functions replacing the original Green's function.

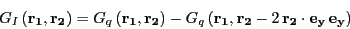$$G _{I} \left( \mathbf{r _{1}},\mathbf{r _{2}} \right) = G _... ...hbf{r _{2}} \cdot \mathbf{ e _{y}} \mathbf{ e _{y}} \right)$$ (7)

The resultant potential is zero everywhere on the x axis, which corresponds with the ground plane. The potential at infinity is zero in all directions moving away from the origin because the Green's functions from each conductor and its corresponding image conductor tend to cancel.