Electric currents and the inductance matrix

Of course, charges are not the only source terms in the electromagnetic field equations. The other important source terms are electric currents. They give rise to another potential, called the magnetic vector potential. The magnetic field can be deduced from the vector potential. The magnetic vector potential depends on its source terms in basically the same way that the scalar potential depends on its source terms (for details of this dependence, see the Feynman Lectures on Physics, Volume 2, Table 15-1). The only difference is that in the latter case there is a division of the currents by a factor of the square of the velocity of light. If the problem is two dimensional, and the currents are in the same places as the charges, then the way that magnetic vector potential depends on currents is essentially the same as the way that scalar potential depends on charges. This dependence can be expressed in terms of the inductance matrix.

$$\mathbf{L} = c ^{-2} \left[ G _{I} \right]$$ (10)

Since the capacitance matrix is obtained by inverting this dependence, it follows that the capacitance matrix and inductance matrix are essentially inverse. The product of the inductance matrix and the capacitance matrix, multiplied by the square of the speed of light, is equal to the identity matrix.

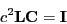$$c ^{2} \mathbf{L} \mathbf{C} = \mathbf{I}$$ (11)