Conductor radius

Properly the Green's function corresponds with charge density. The potential is obtained by multiplying the Green's function by the charge density, and integrating this over all volumes containing non-zero charge densities. In the overhead line problem, it is normal to replace charge density by charge per unit length on each line. Provided that the lines are well separated, and that the potential is evaluated at a place not on or within a line, this produces a satisfactory result. However some care is required to evaluate the potential on a line due to charges on that line. The charges exist entirely on the surface of the conductor. In that case the potential due to those charges becomes steadily greater (assuming that the total charge on the surface is positive) towards the surface of the conductor, reaching a maximum value at that surface. Inside the conductor it does not change, for if it did, then there would be an electric field inside the conductor and the charges would move to negate it. The top of the potential hill is flat. The equivalent formula for the Green's function due to the surface charges is

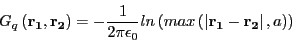$$G _{ q } \left( \mathbf{r _{1}},\mathbf{r _{2}} \right) = -... ...mathbf{r _{1}}-\mathbf{r _{2}} \right\vert , a \right) \right)$$ (2)

where a represents the conductor radius.