

Kabculus home page
Next: The ground plane
Up: Conductor radius
Previous: Conductor radius
It is quite common for overhead lines to consist of bundles of conductors.
Each bundle is
held together with spacing frames, and these frames are located at regular intervals along the route.
A bundle typically contains two or four conductors.
The frames are ordinarily small compared with the line separation.
However the potential on any conductor in a bundle is influenced by the charges on the other
conductors in the bundle.
The charge divides equally between the conductors.
The potential on any conductor in a twin conductor bundle is then (ignoring all other bundles)
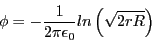 |
(3) |
where 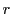 is the conductor radius and
is the conductor radius and 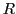 is the radius of the bundle circle
(which contains all the centres of the conductors in that bundle).
Hence the equivalent radius of a single conductor is given by
is the radius of the bundle circle
(which contains all the centres of the conductors in that bundle).
Hence the equivalent radius of a single conductor is given by
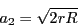 |
(4) |
This expression should then be substituted for 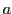 in the expression for the
Green's function
in the expression for the
Green's function 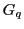 associated with charges on single conductors.
associated with charges on single conductors.
The corresponding potential for a quadruple conductor bundle is
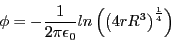 |
(5) |
In this case the equivalent radius of a single conductor is given by
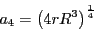 |
(6) |


Kabculus home page
Next: The ground plane
Up: Conductor radius
Previous: Conductor radius
Kabculus 2006-03-30